Theorems on Locus of a Point
Locus is a curve or other figure formed by all the points satisfying a particular equation of the relation between coordinates, or by a point, line, or surface moving according to mathematically defined conditions. A path consisting of a set of points whose location is governed by some definite rule of rules is called locus.
Theorems on Locus of a Point which is Equidistant from Two Fixed Points
The locus of a point which is equidistant from two fixed points is the perpendicular bisector of the line segment joining the two fixed points.
Given,
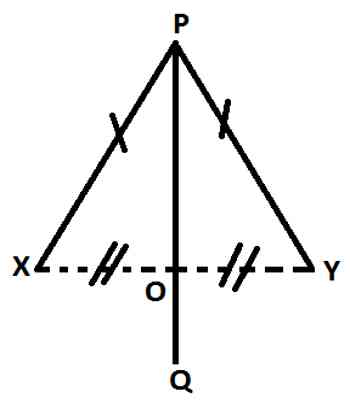
Let X and Y be two given fixed points. PQ is the path traced out by the moving point P such that each point on it is equidistant from X and Y. Therefore, PX = PY.
To prove: PQ is the perpendicular bisector of the line segment XY.
Construction: Join X to Y. Let PQ cut XY at O.
Proof
From △PXO and △PYO,
PX and PY (Given)
XO = YO (Since, every point of PQ is equidistant from X and Y, and O is a point on PQ.)
PO = PO (Common side.)
Therefore, by the SSS criterion of congruency △PXO ≅ △PYO.
Now ∠POX = ∠POY (since, corresponding parts of congruent triangles are congruent.)
Again ∠POX + ∠POY = 180° (Since, XOY is a straight line.
Therefore, ∠POX = ∠POY = 180°/2 = 90°
Also, PQ bisects XY (Since, XO = YO)
Therefore, PQ ⊥ XY and PQ bisects XY, i.e., PQ is the perpendicular bisector of XY (Proved)
Information Source: