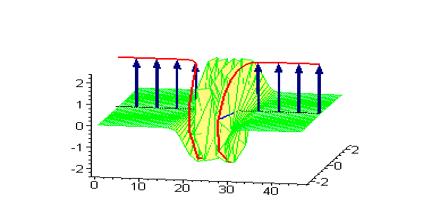
Sine Gordon Equation Is spatiotemporal models of nonlinear excitations in complex physical systems. It was originally introduced by Edmond Bour (1862) in the course of study of surfaces of constant negative curvature as the Gauss–Codazzi equation for surfaces of curvature −1 in 3-space, and rediscovered by Frenkel and Kontorova (1939) in their study of crystal dislocations. It is a nonlinear hyperbolic partial differential equation in 1 + 1 dimensions involving the d’Alembert operator and the sine of the unknown function.
Sine Gordon Equation