Field Line
Definition
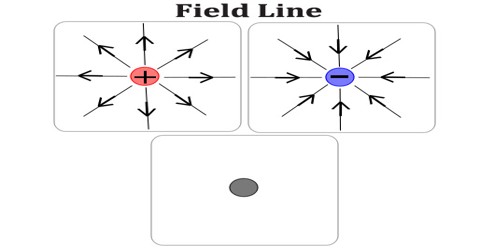
Field Line is a line (line of force), which is used to indicate the direction of a field, especially an electric or magnetic field, at various points in space. The tangent of a line of force at each point indicates the orientation of the field at that point. Arrows are usually used to indicate the direction of the force.
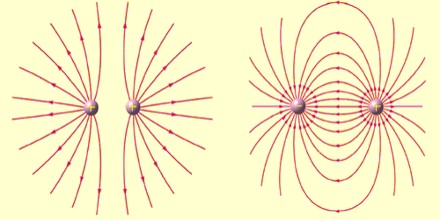
A complete description of the geometry of all the field lines of a vector field is sufficient to completely specify the direction of the vector field everywhere. In order to also depict the magnitude, a selection of field lines is drawn such that the density of field lines at any location is proportional to the magnitude of the vector field at that point. A vector field defines a direction at all points in space; a field line for that vector field may be constructed by tracing a topographic path in the direction of the vector field. More precisely, the tangent line to the path at each point is required to be parallel to the vector field at that point.
If the vector field describes a velocity field, then the field lines follow stream lines in the flow. Perhaps the most familiar example of a vector field described by field lines is the magnetic field, which is often depicted using field lines emanating from a magnet.
The magnetic field direction is the same direction a compass needle points, which is tangent to the magnetic field line at any given point. A magnetic field line can never cross another field line. The magnetic field is unique at every point in space.
Magnetic field lines are continuous and unbroken, forming closed loops. Magnetic field lines are defined to begin on the north pole of a magnet and terminate on the South Pole.
Uses of Magnetic Field Lines
Maxwell gave four Electromagnetic wave equations, and it was said that ‘God ‘ had written these equations. It is one of the best inventions of modern world.
These four equations combinedly confirm relation between electric field and magnetic field. “If there is change is electric fields it create magnetic field and vice versa changing in magnetic fields create electric field”. This is the basis of Electromagnetic theory. This is the basic reason why light travels infinite distance in vacuum.
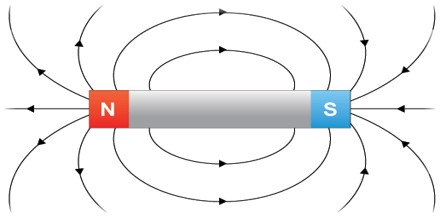
In vacuum when light travels electric filed energy change into magnetic field energy, again magnetic fileds energy convert into electric filed energy and this process goes on till some medium either disturbs this energy oscillation or absorbs this energy.
Light is a types of Electromagnetic waves so all Electromagnetic waves follow same principles but due to their different frequencies there energies and properties are different.
The whole communication world is nothing without this field and other part that is generator that generates power uses magnetic field to generate electric field that is current. So all power plant on the earth except solar uses different sources of energy (fuel) to to move rotar in magnetic field which creates current.
So without Magnetic field we don’t have electric power, communication, induction stove, microwave oven etc. and its uses are unlimited.
Uses of Magnetic field alone are very limited it is very very important when it combines with electric filed.
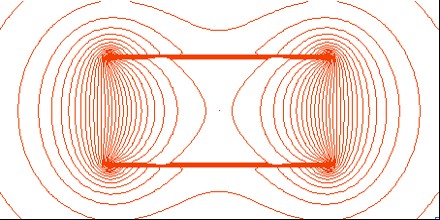
Field Lines can also be used to trace familiar quantities from vector calculus:
The Kelvin–Stokes theorem shows that field lines of a vector field with zero curl cannot be closed loops. In other words, curl is always present when a field line forms a closed loop. It may be present in other situations too, such as a helical shape of field lines.
Divergence may be easily seen through field lines, assuming the lines are drawn such that the density of field lines is proportional to the magnitude of the field. In this case, the divergence may be seen as the beginning and ending of field lines. If the vector field is the resultant of radial inverse-square law fields with respect to one or more sources then this corresponds to the fact that the divergence of such a field is zero outside the sources. In a solenoidal vector field, the field lines neither begin nor end; they either form closed loops, or go off to infinity in both directions. If a vector field has positive divergence in some area, there will be field lines starting from points in that area. If a vector field has negative divergence in some area, there will be field lines ending at points in that area.