Net Present Value (NPV) –
Net present value (NPV) is an investment measure that tells an investor whether the investment is achieving a target yield at a given initial investment. NPV also quantifies the adjustment to the initial investment needed to achieve the target yield assuming everything else remains the same. Formally, the net present value is simply the summation of cash flows (C) for each period (n) in the holding period (N), discounted at the investor’s required rate of return (r):
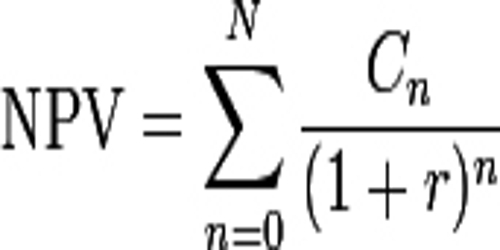
NPV shows the actual benefit received over and above from the investment made in the particular project for the time and risk. Here, one rule of thumb is followed, accept the project with positive NPV, and reject the project with negative NPV. However, if the NPV is zero, then that will be a situation of indifference i.e. the total cost and profits of either option will be equal. The calculation of NPV can be done in the following way:
NPV = Discounted Cash Inflows – Discounted Cash Outflows
Internal Rate of Return (IRR) –
Internal Rate of Return (IRR) for a project is the discount rate at which the present value of expected net cash inflows equates the cash outlays. Put simply, discounted cash inflows are equal to discounted cash outflows. It can be explained with the following ratio, (Cash inflows / Cash outflows) = 1.
At IRR, NPV = 0 and PI (Profitability Index) = 1
In this method, the cash inflows and outflows are given. The calculation of the discount rate, i.e. IRR, is to be made by trial and error method.
IRR is also another term people use for interest. Ultimately, IRR gives an investor the means to compare alternative investments based on their yield. Mathematically, the IRR can be found by setting the above NPV equation equal to zero (0) and solving for the rate of return (IRR).
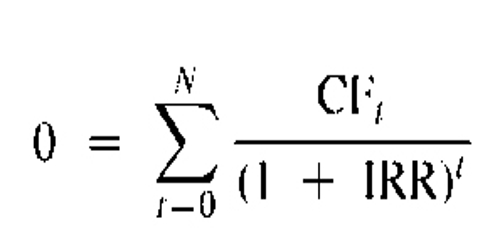
Difference between NPV and IRR –
The basic differences between NPV and IRR are presented below:
- The aggregate of all present value of the cash flows of an asset, immaterial of positive or negative is known as Net Present Value. Internal Rate of Return is the discount rate at which NPV = 0.
- The calculation of NPV is made in absolute terms as compared to IRR which is computed in percentage terms.
- The purpose of the calculation of NPV is to determine the surplus from the project, whereas IRR represents the state of no profit no loss.
- Decision making is easy in NPV but not in the IRR. An example can explain this, In the case of positive NPV, the project is recommended. However, IRR = 15%, Cost of Capital <15%, the project can be accepted, but if the Cost of Capital is equal to 19%, which is higher than 15%, the project will be subject to rejection.
- Intermediate cash flows are reinvested at the cut off rate in NPV whereas in IRR such an investment is made at the rate of IRR.
- When the timing of cash flows differs, the IRR will be negative, or it will show multiple IRR which will cause confusion. This is not in the case of NPV.
- When the amount of initial investment is high, the NPV will always show large cash inflows while IRR will represent the profitability of the project irrespective of the initial investment. So, the IRR will show better results.
Both IRR and NPV can be used to determine how desirable a project will be and whether it will add value to the company. While one uses a percentage, the other is expressed as a dollar figure. While some prefer using IRR as a measure of capital budgeting, it does come with problems because it doesn’t take into account changing factors such as different discount rates. In these cases, using the net present value would be more beneficial.
Net Present Value and Internal Rate of Return both are the methods of discounted cash flows, in this way we can say that both consider the time value of money. Similarly, the two methods, considers all cash flows over the life of the project.
During the computation of Net Present Value, the discount rate is assumed to be known, and it remains constant. But, while calculating IRR, the NPV fixed at ‘0’, and the rate which fulfills such a condition is known as IRR.
Information Sources: