Continuum mechanics is a branch of mechanics that studies the deformation and transmission of forces in materials that are modeled as a continuous mass rather than discrete particles. It is a branch of mechanics that studies the mechanical behavior of materials that are modeled as continuous matter without taking into account their atomic or molecular structure. In the nineteenth century, the French mathematician Augustin-Louis Cauchy was the first to develop such models. It provides a framework for analyzing how materials respond to different mechanical loads and deformations.
The basic assumption in continuum mechanics is that matter can be treated as a continuous medium, which means that properties like density, temperature, and stress are assumed to be well-defined at all points in the material. This assumption allows differential calculus and partial differential equations to be used to describe the material’s behavior.
A continuum model presumes that the object’s substance completely fills the space it occupies. This ignores the fact that matter is made up of atoms, but provides an accurate description of matter on length scales much larger than inter-atomic distances. The concept of a continuous medium enables intuitive analysis of bulk matter through the use of differential equations that describe the behavior of such matter in terms of physical laws such as mass conservation, momentum conservation, and energy conservation. Constitutive relationships express information about the specific material.
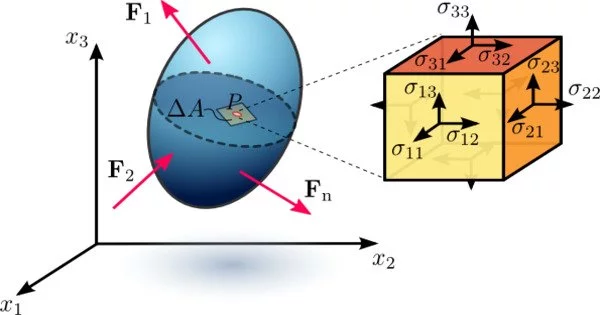
Deformation, stress, and the equations governing material motion are all important concepts in continuum mechanics. Deformation refers to changes in the shape or size of a material element, whereas stress is the internal force per unit area that the material experiences. The equations of motion describe how a material responds to applied forces, such as the Navier-Stokes equations for fluids or the equations of linear elasticity for solids.
Continuum mechanics considers the physical properties of solids and fluids regardless of the coordinate system in which they are observed. Tensors, which are mathematical objects with the distinct property of being independent of coordinate systems, are used to represent these properties. This allows physical properties to be defined at any point along the continuum using mathematically convenient continuous functions. The concepts of continuum mechanics underpin the theories of elasticity, plasticity, and fluid mechanics.
Application
Continuum mechanics is widely used in engineering and physics to investigate a wide range of phenomena, such as the behavior of solids, fluids, and gases under various conditions. It offers a mathematical framework for analyzing structure mechanics, predicting material failure, comprehending fluid flow, and designing mechanical systems. Civil engineering and aerospace engineering are two examples of applications, as are materials science and biomechanics.
Overall, continuum mechanics offers a powerful set of tools for understanding and predicting the mechanical behavior of materials at the macroscopic level, without explicitly considering the behavior of individual atoms or molecules.