Cash flow matching also called dedicating a portfolio, is a process of hedging in which a company or other entity matches its cash outflows (i.e., financial obligations) with its cash inflows over a given time horizon. It is a subset of immunization strategies in finance. Cash flow matching is of particular importance to defined benefit pension plans.
Cash flow matching involves investing in certain securities with a certain expected return so that the investor will be able to pay for future liabilities. Pension funds and annuities perform the most cash-flow matching, as they have future liabilities that are both large and relatively easy to estimate. Portfolios that perform cash-flow matching usually invest in low-risk, investment-grade securities.
Businesses do need to pay obligations or access cash flow for a variety of reasons. Keeping money in a reserve account helps with this process. Low-interest accounts, however, do not provide a dynamic means in which to cover obligations when future cash flow is limited. Interest-bearing accounts might be needed to address the situation.
Classical Cash Flow Matching – The classical cash flow matching problem can be formulated as the following LP:
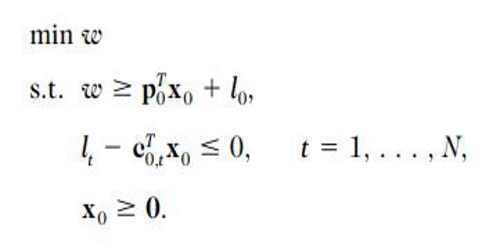
The classical cash flow matching problem involves computing the minimum cost portfolio with no shortfall over time, that is, lt – CTo,t xo ≤ o for all t. However, if the liabilities span a time horizon longer than the maturities of the available bonds, the cash flow matching problem will be infeasible. We consider a risk management approach where we reformulate the problem to that of minimizing the cost of the portfolio while controlling the shortfall risk and reinvestment risk at a specified level.
It is possible to solve the simple cash flow matching problem using linear programming. Suppose that we have a choice of j = 1,…,n bonds with which to receive cash flows over t = 1,…,T time periods in order to cover liabilities L1,…,LT for each time period. The jth bond in time period t is assumed to have known cash flows Ftj and initial price pj. It possible to buy xj bonds and to run a surplus st in a given time period, both of which must be non-negative, and leads to the set of constraints:
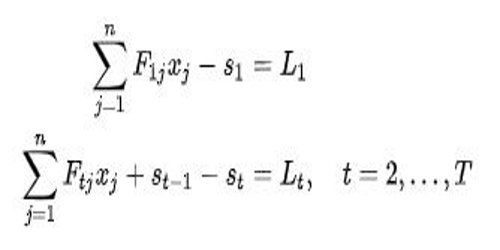
Cash-flow matching is one of two kinds of structured portfolio strategies (the other is immunization), and it is intended for investors who need to fund a series of future expenses. The immunization strategy is generally for investors who need to fund one lump-sum future liability or expense.
To implement the cash-flow matching strategy, we first need to project our future cash needs. In the example below, we need $30,000 in Year 1, $40,000 in Year 2, and $50,000 in Year 3.
Next, we buy a 3-year bond (Bond A) that will return enough principal and interest to cover our expenses in Year 3. Assuming that rates are 11.11% for a 3-year bond, we need to invest $45,000 today to cover our cash needs in Year 3.
Most bonds throw off bonds every year, and assuming Bond A is no exception, we can expect to receive interest payments in Years 1 and 2. These interest payments will offset a portion of our cash needs for those years.
After accounting for the interest from Bond A, we’re still $35,000 short in Year 2. So now we need to figure out how much to invest in a 2-year bond (Bond B) to reach our $35,000 goal. Following the same steps we used above, we can figure out the interest payments and principal amounts needed to meet our cash needs for Years 1 & 2.
Our goal is to minimize the initial cost of purchasing bonds to meet the liabilities in each time period, given by pTx. Together, these requirements give rise to the associated linear programming problem:
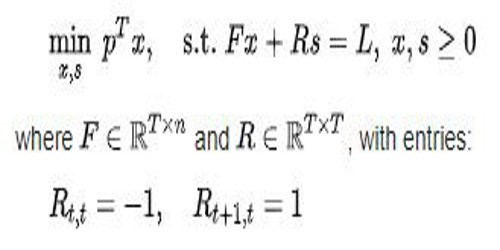
In the instance when fixed income instruments (not necessarily bonds) are used to provide the dedicated cash flows, it is unlikely to be the case that fractional components are available for purchase. Therefore, a more realistic approach to cash flow matching is to employ mixed-integer linear programming to select a discrete number of instruments with which to match liabilities.
Information Sources: