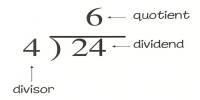Statistical Mean
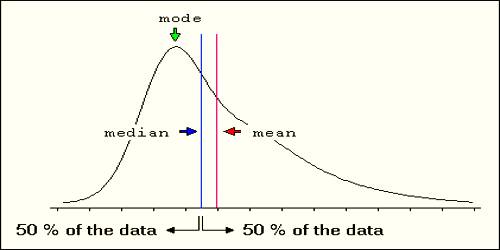
The statistical mean refers to the mean or average that is used to derive the central tendency of the data in question. It is determined by adding all the data points in a population and then dividing the total by the number of points. The resulting number is known as the mean or the average.
For example, the mean mark obtained by students in a test is required to correctly gauge the performance of a student in that test. If the student scores a low percentage but is well ahead of the mean, then it means the test is difficult and therefore his performance is good, something that simply a percentage will not be able to tell.
In statistics, the mean is the average of a set of data. To find the mean, sum all the numbers and then divide by the number of items in the set. For example, to find the mean of the following set of numbers: 21, 23, 24, 26, 28, 29, 30, 31, 33
First add them all together:
21 + 23 + 24 + 26 + 28 + 29 + 30 + 31 + 33 = 245
Then divide your answer by the number of items in your set. There are 9 numbers, so:
245 / 9 = 27.222
The statistical mean is commonly called the average.
Another Example:
For example, let’s say you have four test scores: 15, 18, 22, and 20. To find the average, you would first add all four scores together, then divide the sum by four. The resulting mean is 18.75. Written out, it looks something like this:
(15 + 18 + 22 + 20) / 4 = 75 / 4 = 18.75
If you were to round up to the nearest whole number, the average would be 19.
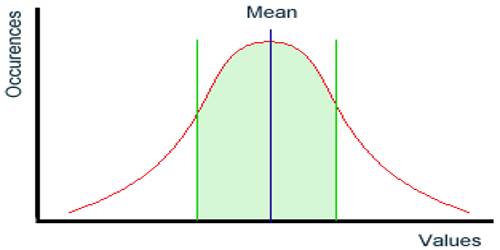
To find the mean of a group of numbers:
- Add the numbers together
- Divide by how many numbers were added together
The mean is the average of all numbers and is sometimes called the arithmetic mean. To calculate mean, add together all of the numbers in a set and then divide the sum by the total count of numbers. For example, in a data center rack, five servers consume 100 watts, 98 watts, 105 watts, 90 watts and 102 watts of power, respectively. The mean power use of that rack is calculated as (100 + 98 + 105 + 90 + 102 W)/5 servers = a calculated mean of 99 W per server.
Note: The word “mean” can have other interpretations outside of statistics. For example, when the weather service reports that a “mean daily temperature” is 75 degrees, that number was obtained by taking the sum of the high daily temperature and the low daily temperature and dividing by 2. This is what is called a “Midrange“. While this can be a cause of confusion, remember that in statistics, the mean is the average.
Information Source: