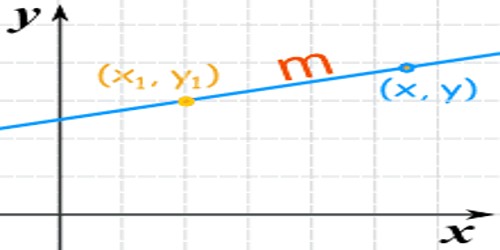Point-slope Form of a Line
Slope-intercept form is useful when we know the y- intercept of a line. However, we are not always given this information. When we know the slope and one point which is not the y -intercept, we can write the equation in point-slope form.
To find the equation of a straight line passing through a fixed point and having a given slope,
Let AB be the line passing through the point (x1, y1), and let the line be inclined at an angle θ with the positive direction of the x-axis.
Then, tan θ = m = slope.
Let the equation of the line be y = mx + c, ……………. (i)
where m is the slope of the line and c is the y-intercept. As A (x1, y1) is a point on the line AB (x1, y1) satisfy (i).
Therefore, y1 = mx1 + c …………………. (ii)
Subtracting (ii) from (i)
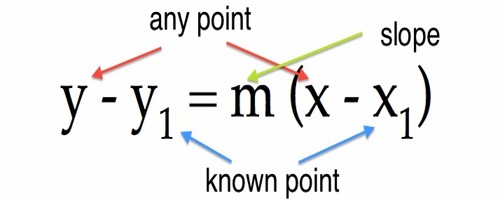
y – y1 = m(x – x1)
The equation of a line passing through(x1, y1) and having the slope m is y – y1 = m(x – x1).
The equation is useful when we know:
- one point on the line
- and the slope of the line, and want to find other points on the line.
For example:
The equation of a line passing through the point (0, 1) and inclined at 30° with the positive direction of the x-axis is y – 1 = tan 30° ∙ (x – 0) or y – 1 = x/√3
Remember:
(i) Equation of the y-axis:
The y-axis passes through the origin (0,0) and inclined at 90° with the positive direction of the x-axis.
So, the equation of the y-axis is y – 0 = tan 90° ∙ (x – 0)
⟹ y = ∞ ∙ x
⟹ y/∞ = x
⟹ x = 0
The coordinate of any point on the y-axis is (0, k), where k changes from point to point. Thus, the x-coordinate of any point on the y-axis is 0 and so the equation x = 0 is satisfied by the coordinates of any point on the y-axis. Therefore, the equation of the y-axis is x = 0.
(ii) Equation of a line parallel to the y-axis:
Let AB be a line parallel to the y-axis. Let the line be at a distance a from the y-axis. Then, the slope = tan 90° = ∞ and the line passes through the point (a, 0).
Therefore, the equation of AB is y – 0 = tan 90° ∙ (x – a)
or, y cot 90° = x – a
⟹ y × 0 = x – a
⟹ x – a = 0
⟹ x = a
Information Source: