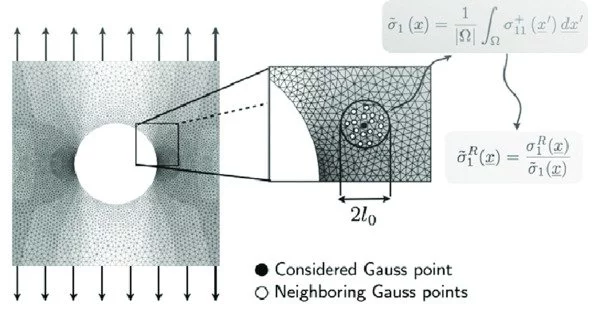
A new theoretical study provides a framework for understanding nonlocality, a property that quantum networks must have in order to perform operations that conventional communications technology cannot. Researchers determined the conditions required to create systems with strong, quantum correlations by clarifying the concept.
The study, published in Physical Review Letters, adapts quantum computing theory techniques to develop a new classification scheme for quantum nonlocality. This not only allowed the researchers to unify previous studies of the concept into a common framework, but it also facilitated the proof that networked quantum systems can only exhibit nonlocality if they have a specific set of quantum features.
“On the surface, quantum computing and nonlocality in quantum networks are different things, but our study shows that, in certain ways, they are two sides of the same coin,” said Eric Chitambar, a professor of electrical and computer engineering at the University of Illinois Urbana-Champaign and the project lead. “In particular, they require the same fundamental set of quantum operations to deliver effects that cannot be replicated with classical technology.”
Our result is the quantum network analogue to an important quantum computing result called the Gottesman-Knill theorem. While Gottesman-Knill clearly defines what a quantum computer must do to surpass a classical one, we show that a quantum network must be constructed with a particular set of operations to do things that a standard communications network cannot.
Gatto Lamas
Nonlocality is a result of entanglement, in which quantum objects maintain strong connections despite being separated by vast physical distances. When entangled objects are used to perform quantum operations, statistical correlations emerge that cannot be explained by non-quantum means. Nonlocal correlations are defined as such. To perform truly quantum functions, a quantum network must have some degree of nonlocality, but the phenomenon is still poorly understood.
Chitambar and physics graduate student Amanda Gatto Lamas used quantum resource theory formalism to study nonlocality. By treating nonlocality as a “resource” to be managed, the researchers’ framework enabled them to see previous nonlocality studies as distinct instances of the same concept, albeit with different constraints on the resource’s availability. This aided in the demonstration of their main result, which is that nonlocality can only be achieved using a limited set of quantum operations.
“Our result is the quantum network analogue to an important quantum computing result called the Gottesman-Knill theorem,” Gatto Lamas explained. “While Gottesman-Knill clearly defines what a quantum computer must do to surpass a classical one, we show that a quantum network must be constructed with a particular set of operations to do things that a standard communications network cannot.”
Chitambar believes that the framework will be useful not only for developing criteria to assess the quality of a quantum network based on its degree of nonlocality, but also for expanding the concept of nonlocality.
“Right now, there is a relatively good understanding of the type of nonlocality that can emerge between two parties,” he explained. “However, for a quantum network with many connected parties, one can imagine that there might be some kind of global property that you can’t reduce to individual pairs on the network.” Such a property could be highly dependent on the overall structure of the network.”