Macaulay duration, also known as a term to maturity or average life, is the weighted average maturity of cash flows, in which the time of receipt of each payment is weighted by the present value of that payment. It is named after Frederick Macaulay, who originated the idea. It is expressed in years, and the weight of each cash flow is calculated by dividing the cash flow’s current value by the price. Portfolio managers that utilize an immunization approach typically use Macaulay duration.
The Macaulay duration of a bond is proportional to its time to maturity and inversely proportional to its coupon rate and interest rate. It is widely used by traders as a measure of cash flow volatility in relation to prices, and it is expressed in years. The sensitivity of a bond’s price to interest rate changes is measured by modified duration. Volatility is a risk indicator that shows how much bond portfolio cash flows change over time.
Macaulay Duration is a vital factor to consider prior to purchasing an obligation instrument. It is utilized as a device to adjust and support bond portfolios against the danger related with changes in bond incomes. The denominator is the amount of the loads, which is definitively the cost of the bond. Consider a collection of predetermined cash flows. As a result, Macaulay duration is determined by adding all the multiples of the present values of cash flows and the associated time periods, then dividing the total by the market bond price.
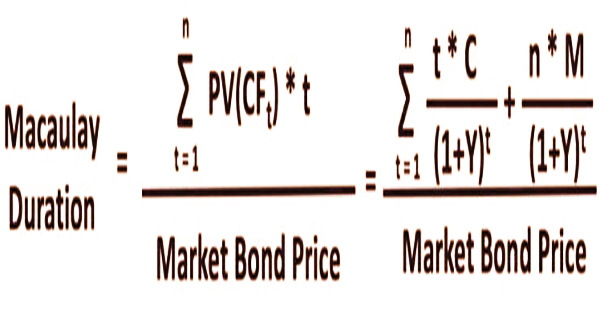
Where:
PV(CFt) – Present value of cash flow (coupon) at period t
t – Time period for each cash flow
C – Periodic coupon payment
n – Total number of periods to maturity
M – Value at maturity
Y – Periodic yield
If and only if there is a single payment at maturity, the Macaulay duration will equal the ultimate maturity. It may be thought of as a set of cash flows’ economic balancing points. One more approach to decipher the measurement is that it is the weighted normal number of years that a financial backer should keep a situation in the bond until the current worth of the bond’s income rises to the sum paid for the bond. Made by Frederick Macaulay in 1938, Macaulay term was not broadly utilized until the 1970s.
With the wide range of various components steady, a bond with a more drawn out term to development accepts a more prominent Macaulay length, as it takes a more extended period to get the important installment at the development. Obviously, security costs are conversely identified with loan fees. If investors know the Duration of the various coupon bonds as well as the expected interest rate structure, they may obtain a good notion of which bond to buy, longer-term or shorter-term.
A bond’s term is also reduced by a sinking fund, a planned prepayment before maturity, and call clauses. The coupon rate and Macaulay duration have an inverse relationship. The lower the term, the bigger the coupon payments, with larger cash amounts paid in the early stages. There are a few distinct kinds of duration to include: key-rate, changed, and compelling. All actions are communicated in years. The thing that matters is standing out every estimation represents changes in financing costs or other installed alternatives in the bond.
Comparing and understanding Macaulay The duration of the instruments might help you decide which ones are best for your fixed-income portfolio. When compared to coupon bonds, a zero-coupon bond has the longest Macaulay duration, providing all other characteristics are identical. It is equivalent to the development for a zero-coupon bond and is not exactly the development for coupon bonds. Securities with a more drawn-out term to development convey more danger and have more income vacillations in light of changes in financing costs.
Bond price and yield have a convex relationship rather than a linear one. This convexity indicates that when yields rise, the gap between real and anticipated prices increases. Modified duration, unlike Macaulay duration, which measures the average time to receive the present value of cash flows corresponding to the current bond price, determines the bond price’s sensitivity to interest rate changes. It’s vital to understand how interest rate fluctuations impact bond prices in order to grasp the notion of Macaulay duration.
Macaulay Duration information is fundamental in learning the future gets back from fixed pay instruments. The adjusted term can be determined by partitioning the Macaulay span of the security by 1 or more the intermittent loan cost, which implies a bond’s Modified length is by and large lower than its Macaulay term. The modified duration of a bond equals the Macaulay duration if it is constantly compounded.
Bonds that trade at a higher price than par, or future value, are said to be trading at a premium. This also implies that current interest rates are lower than the interest rate paid on bonds. Accordingly, it is exceptionally fitting for financial backers, particularly hazard disinclined financial backers, to evaluate and think about the term presented by the different bonds to arrive at any rate fluctuation blend and draw greatest gets back with the least danger conceivable.
By coordinating with the lengths between the resources and liabilities in an organization’s portfolio, the adjustment of financing cost will move the worth of resources and the worth of liabilities by the very same sum, yet in inverse headings. The Macaulay duration may be easily deduced. In general, if a bond’s yield increases by 200 basis points or 2.0 percent, the bond’s duration or life shortens by a specific number of years. The disadvantage of duration-matching is that it only protects the portfolio from modest interest rate swings. For substantial interest rate fluctuations, it is less effective.
Information Sources:
















