The knot theory is based on Lord Kevin’s 1867 proposal that atoms are made of vortex rings or knots. Despite the fact that the hypothesis was proven incorrect, the knot theory has since spread throughout mathematics and physics. Torus knots are a unique type of knot that consists of disjointed and linked closed loops that nest to form complete ring tori. The torus knot is a good candidate for creating hopfions, which are three-dimensional (3D) topological states that resemble particle-like objects, according to physicists.
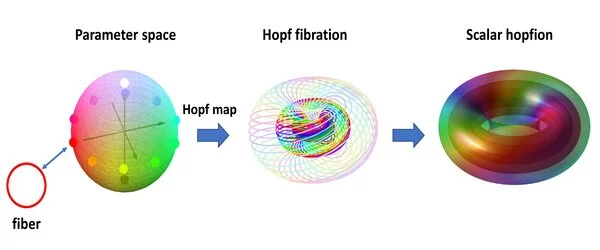
Hopfions are named after Heinz Hopf, who discovered the Hopf fibration in 1931. The preimages of any arbitrary points in S₂ are disjoint and interlinked circles (S₁) in S₃. The S₃ that resides in four-dimensional space can be “seen” by stereographic projection, and the topological features of linkedness of closed loops are preserved.
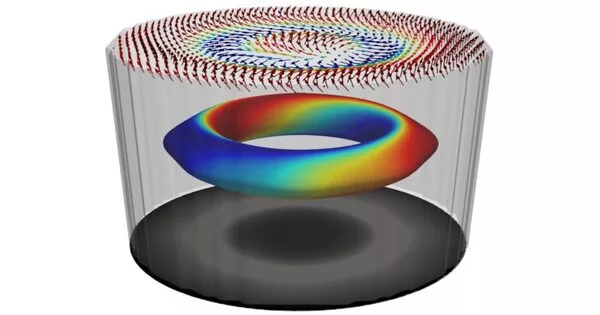
In a new paper published in eLight, a team of scientists, led by Professor Qiwen Zhan from the University of Shanghai for Science and Technology, have demonstrated dynamic scalar optical hopfions in the shape of a toroidal vortex. The “Scalar Optical Hopfions” paper showed how these toroidal vortices could be expressed as an approximate solution for Maxwell’s equations. This research could find applications in artificial materials, nanostructures, and optical communication.
The search for hopfions in physical systems started with the seminal work of Korepin and Faddeev. After nearly half a century, hopfions have been unveiled in various branches of science. Hopf structures have been discovered within superfluid helium as particle-like objects with finite dimensions and energy.
Null solutions to Maxwell’s equations show that electromagnetic field lines, spin or polarization vectors can be tied together using the Hopf fibration to form various knots and links that can be used as information carriers.
The search for hopfions in physical systems started with the seminal work of Korepin and Faddeev. After nearly half a century, hopfions have been unveiled in various branches of science. Hopf structures have been discovered within superfluid helium as particle-like objects with finite dimensions and energy.
Vortex lines in fluids appear in Hopf topological structures, and the linkedness and knottedness of inviscid fluids are conserved. Hopf links are formed by tweezing topological defect lines in liquid crystals. The hopfions mentioned above are vector hopfions, which means that each point in S2 corresponds to a vector with multiple degrees of freedom.
On the contrary, each point in S₂ of scalar hopfions is distinguished by the value of a scalar parameter. The corresponding preimage is a closed loop consisting of all points having the same scalar value. Scalar hopfions have been predicted and are believed to be experimentally feasible in a Bose-Einstein condensate (BEC) controlled by inhomogeneous magnetic fields or in a rotating trapped atomic BEC.
The proposed concept of scalar optical hopfions is spatiotemporally structured pulse propagating in space-time. It provides an additional dimension (time) to encode and transfer topological information. The dynamic scalar optical hopfion is a traveling wave packet in the shape of a toroidal vortex. Scalar optical hopfions are weaved by nested equiphase lines corresponding to one complex knot or several unknotted and interlinked closed loops.
The linking number of two equiphase lines is governed by the Hopf invariant, which is the product of the winding numbers. All equiphase lines form an infinite number of layers of complete ring tori. The discovery of scalar optical hopfions may spur interest in exploring novel methods for light-matter interaction, optical metrology, information encoding, and optical manipulation.
Characterizing a scalar optical hopfion is a challenging task requiring high-resolution and full 3D phase measurement of an ultrafast wave packet. Limited by existing capabilities, we perform two-dimensional phase measurement of the poloidal spiral phase through interfering with the hopfion wave packet (l₁ = 1, l₂ = 1) with a transform-limited reference pulse split from the source.
The reference pulse is considerably shorter in time and interferes with each temporal slice of the hopfion wave packet with the help of an electronically controlled precision stage. The poloidal phase is theoretically a spiral phase in the spatiotemporal domain. Eight spots at equally-spaced toroidal angles are chosen, and the interference patterns at these spots are analyzed.
The orientations of mirrors are carefully adjusted so that the fringes are parallel to the specified toroidal angle. As the reference pulse interferes with the head of the hopfion wave packet, the fringe patterns are straight. The fringes start to bend when approaching the center of the spatiotemporal vortex. When the temporal slice coincides with the vortex core, the upper and lower fringes are shifted by half a period.
As the temporal slicing continues, the fringes bend in the opposite direction and become straight again as the slicing approaches the tail of the hopfion wave packet. Based on the fringe patterns, the poloidal spiral phase can be reconstructed. The toroidal spiral phase is a spatial spiral phase applied by SLM3 and assumed to be perfect in this case due to the difficulties of fully resolving the 3D details of the phase distributions of the entire wave packet.
The total phase is the sum of the poloidal phase and the toroidal phase. The topological features of a scalar optical hopfion are presented.
In summary, a dynamic scalar optical hopfion model is proposed, with its analytical expression provided as an approximate solution to Maxwell’s equations. The equiphase lines are disjoint and linked closed loops in the form of links and knots with a linking number determined by the Hopf invariant, according to numerical simulations and experimental data.
All equiphase loops join together to form complete tori that fill the entire 3D space. The photonic testbed for studying topological states that resemble particle-like objects is provided by dynamic scalar optical hopfions. They could be used for spatiotemporal mode excitation in artificial materials and nanostructures. As high-dimensional information carriers, optical communication offers additional opportunities.