Optical resonances in a Möbius strip can be determined by the topology of the strip, as well as the properties of the materials used to create it. The Möbius strip has a unique topology, characterized by its twisted, non-orientable surface, which can lead to interesting optical phenomena.
In the current issue of Nature Photonics, Prof. Dr. Oliver G. Schmidt, head of the Professorship of Material Systems for Nanoelectronics and Scientific Director of the Research Center for Materials, Architectures and Integration of Nanomembranes (MAIN) at Chemnitz University of Technology, Dr. Libo Ma from the Leibniz Institute for Solid State and Materials Research (IFW) Dresden, and other cooperation partners present a strategy for observing and manipulating the optical Berry phase in Möbius ring microcavities.
They describe how an optical Berry phase can be produced and observed in dielectric Möbius rings in their research report. The first experimental demonstration of a changeable Berry phase for linearly or elliptically polarized resonant light is also provided by them.
Fascinating Möbius strip
Möbius strips are intriguing objects. When you twist two ends of a strip of paper by 180 degrees and join them, you can quickly make a Möbius strip. You notice that this ribbon has only one surface upon closer investigation. One cannot discern between inside and outside, or below and above, and it cannot be orientated.
The Möbius strip has been the subject of innumerable mathematical discussions, artistic representations, and practical uses because of this unique “topological” quality, such as in paintings by M.C. Escher, as a wedding ring, or as a drive belt to wear both sides of the belt equally.
Optical ring resonators
Closed bands or rings also play an important role in optics and optoelectronics. To date, however, they have not been built of paper or Möbius strips but rather of optical materials like silicon and silicon dioxide or polymers. These “normal” rings are micrometers in size rather than centimeters.
Optical resonances happen when light of a certain wavelength travels in a tiny ring due to constructive interference. The shorter the string, the shorter the wavelength, and the higher the tone, the diverse tones it produces at different lengths serve as an example of this principle.
Exact optical resonance or constructive interference happens when the ring’s circumference is a multiple of the light’s wavelength. In these circumstances, the ring is referred to as an optical ring resonator because the light echoes within it.
In contrast, when the ring’s circumference is an odd multiple of half the light’s wavelength, the light is greatly attenuated, and destructive interference results. The result is that an optical ring resonator severely attenuates light of other wavelengths that does not “fit” in the ring while strongly enhancing light of some wavelengths.
In terms of technology, the ring resonator functions as an optical filter that can selectively “sort” and process light when it is incorporated on a photonic chip. Modern data transmission networks’ optical signal processing relies heavily on optical ring resonators.
How polarized light circulates in the Möbius strip
Polarization, in addition to wavelength, is a crucial aspect of light. Different polarizations of light are possible, such as linear or circular polarization. When light travels through an optical ring resonator, its polarization does not alter and stays the same across the entire ring.
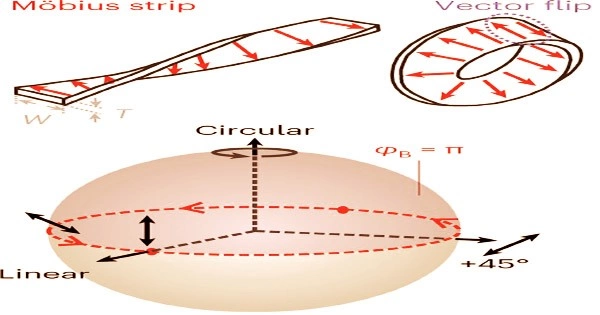
If a Möbius strip or, better still, a Möbius ring is used in place of the optical ring resonator, the situation is drastically altered. It is helpful to think about the specifics of the Möbius ring’s geometry in order to comprehend this instance more fully. A Möbius ring’s cross-section resembles a thin strip of paper, with two of its edges significantly longer than its two adjacent edges.
Let us now assume that linearly polarized light circulates in the Möbius ring. The polarization continuously rotates up to 180 degrees when going entirely around the Möbius ring because it tends to align itself in the direction of the long cross-sectional side of the Möbius ring. The polarization of the light is always maintained in “normal” ring resonators, which is a significant difference. And that’s not all.
The optical resonances now happen at odd multiples of half the wavelength rather than at full wavelength multiples that fit into the ring because the twisting of the polarization changes the phase of the light wave.
Part of the research group had already predicted this effect theoretically in 2013. This prediction, in turn, is based on work by physicist Michael Berry, who introduced the eponymous “Berry phase” in 1983, describing the change in the phase of light whose polarization changes as it propagates.
First experimental evidence
The Berry phase of light moving around a Möbius ring is experimentally unveiled in the most recent study to appear in Nature Photonics. Two rings of the same diameter were created for this purpose. The first is a “normal” ring and the second is a Möbius ring.
And as expected, compared to the “normal” ring, the optical resonances in the Möbius ring appear at various wavelengths. However, the experimental outcomes go much beyond what was initially anticipated. For instance, the linear polarization spins and also takes on an increasingly elliptical shape. The resonances almost always occur at non-integer multiples of half the wavelength, though not precisely at odd multiples. Möbius rings with decreasing strip width were created in an effort to determine the cause of this aberration.
According to this study, the ellipticity of the polarization and the deviation of the resonance wavelength from the “normal” ring weakened over the course of the narrowing Möbius strip. This is simple to understand because when the band’s breadth equals its thickness, the Möbius ring’s unique topological qualities combine with those of a “normal” ring. This implies, however, that the Berry phase in Möbius rings can be easily regulated by altering the band’s style.
Optical Möbius rings have some exciting new fundamental features, and new technology applications are also emerging. The tunable optical Berry phase in Möbius rings could support quantum logic gates in quantum computation and simulation and be used for all-optical data processing of qubits and classical bits.
Additionally, the unique topology of the Möbius strip can also affect the way light propagates through the strip, leading to unique optical properties that may have potential applications in areas such as sensing and communication.