Effective Duration assesses the price sensitivity of hybrid security (bond and option) to a change in the benchmark yield curve by measuring the duration of the security with options incorporated. This duration measure is a risk indicator because it accounts for the fact that projected cash flows will fluctuate when interest rates change. Estimating the percentage change in a bond’s price versus a benchmark yield curve, such as a government par curve, is one approach to analyze a bond’s risk.
If a bond with embedded options behaves like an option-free bond, effective duration may be calculated using modified duration. It is similar to modified duration, but the denominator for both calculations is different. Incomes are unsure in securities with implanted alternatives, making it hard to know the pace of return. The effect on incomes as financing costs change is estimated by compelling span. The changed span can be known as a yield term, while the powerful length is a bend span.
For hybrid instruments, which may be split into a bond and an option, the effective duration figure is utilized (callable bonds). It predicts how much a bond’s price will fall if interest rates climb by 1%. Embedded bonds make it more difficult for investors to calculate the internal rate of return since cash flows are more unpredictable. The idea of effective duration comes into play at this point.
Effective Duration Formula:
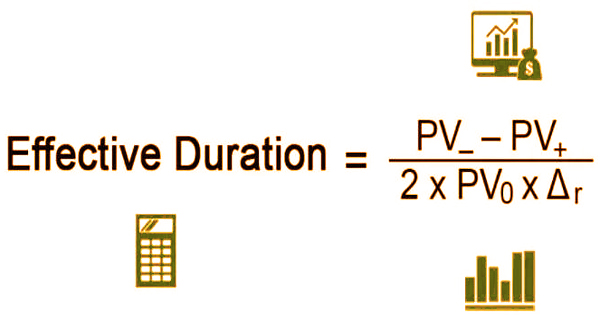
Where,
PV– = Present value of expected cash flows if the yield falls by r basis points.
PV+ = Present value of expected cash flows if the yield increases by r basis points.
PV0 = Present value of expected cash flows when no change in yield.
Δr = Change in yield.
The effective duration also aids in calculating interest rate volatility in respect to the yield curve, and hence projected bond cash flows. In 1983, economist Frederick Macaulay devised a method for calculating a bond’s price volatility known as the “Macaulay Duration.” Despite its effectiveness, the technique was not given much weight until the 1970s, when interest rates began to fluctuate.
Many investors at the time need a tool to assist them to analyze the volatility of their fixed-income assets. It led to the creation of the term “modified duration,” which offered a more accurate means of calculating shifting bond prices. When interest rates plummeted in the mid-1980s, investment banks devised “effective duration” or “options adjusted duration,” which estimated price fluctuations depending on the bond’s call characteristics.
The worth of the successful length will consistently be lower than the development of the bond. The greatest impediment of compelling length measure is its guess. It contrasts from an adjusted length in light of the fact that the last estimate the yield span the unpredictability of the loan fees as far as the security’s respect development while powerful term estimates the bend term, which computes the financing cost instability utilizing the yield bend as a benchmark.
When executing the embedded option would provide no advantage to the investor, a bond with embedded options functions as an option-free bond. The rise or reduction in rate is considered to be constant in both directions and a price is calculated, however, the change in interest rate might be variable and have a different influence on the price. As a result, a change in yield is unlikely to affect the security’s cash flows.
For example, if current interest rates are 10% and a callable bond pays a monthly of 6%, the callable bond will act like an option-free bond since it would be inefficient for the business to call the bond and reissue it at a higher interest rate.
Furthermore, if interest rates remain constant and the issuer’s credit rating improves, the issuer will be able to get credit at a lower cost, triggering a call execution and redemption. Such factors, however, are not taken into account when the calculations are made.
Duration is essential to financial backers for quite some time. It is a useful apparatus to survey the financing cost hazard of a bond and can be utilized as a feature of hazard evaluation alongside the credit hazard and liquidity of the bond. Effective Duration is useful for determining the interest rate sensitivity of hybrid instruments. It demonstrates how sensitive a bond is to changes in market returns for similar risk bonds.
Investors can build their portfolios to profit from interest rate changes by properly predicting the effect of a market shift on bond prices. The measure is a frequently used model for option integrated asset-liability management, despite the fact that it is an approximation. It can also assist them in managing their future cash flows and risk-protecting their assets.
Information Sources: