Addition equations with two digit integers
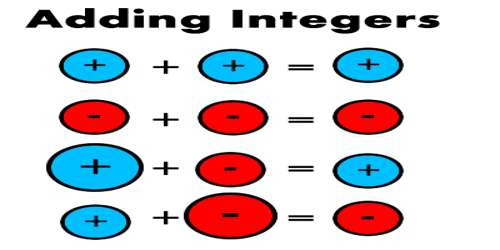
An addition equation is a problem that has two or more numbers or integers added together and equaling another integer. For example, 12 + 11 = 23 is an equation. But for our maze game, we are actually missing an integer. So instead of seeing 12 + 11 = 23, you will see 12 + x = 23. An x is usually used to represent a missing value. It is then your job to find out what this missing integer is. How do you go about doing that?
An equation is a mathematical statement that has an expression on the left side of the equals sign (=) with the same value as the expression on the right side. An example of an equation is 20 + (- 60) = – 40.
One of the terms in an equation may not be known and needs to be determined. The unknown term may be represented by a letter such as x (e.g. 2 + x = – 4). The equation is solved by finding the value of the unknown x that makes the two sides of the equation have the same value. One of the terms in an equation may not be know and needs to be determined. Often this unknown term is represented by a letter such as x. (e.g. 20 + x = – 40).
The solution of an equation is finding the value of the unknown x. To find the value of x we can use the subtractive equation property which says: “The two sides of an equation remain equal if the same number is subtracted from each side.” We may also use the additive equation property which says: “The two sides of an equation remain equal if the same number is added to each side.”
Example:
– 50 + x = 40
– 50 + x + 50 = 40 + 50
0 + x = 90
x = 90
Check the answer by substituting the answer (90) back into the equation.
– 50 + 90 = 40
Information Source: