Volume of a Cone
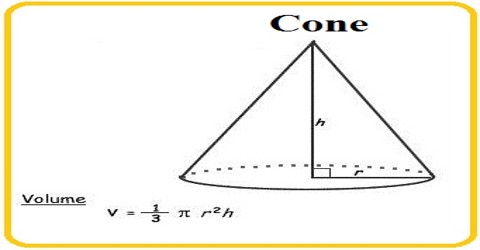
A cone is a three-dimensional figure with one circular base. A curved surface connects the base and the vertex. The volume of a 3 -dimensional solid is the amount of space it occupies. Volume is measured in cubic units ( in3, ft3, cm3, m3 etc cetera).
The volume of a cone is: 1/3(Area of Base)(height) = 1/3 π r2 h
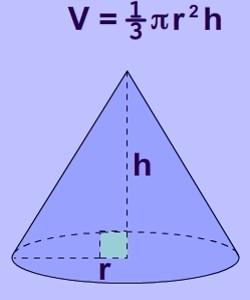
The volumes of a cone and a cylinder are related in the same way as the volumes of a pyramid and a prism are related. If the heights of a cone and a cylinder are equal, then the volume of the cylinder is three times as much as the volume of a cone.
Example:
Find the volume of the cone shown. Round to the nearest tenth of a cubic centimeter.
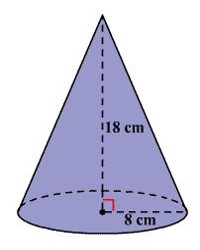
Solution
From the figure, the radius of the cone is 8 cm and the height is 18 cm.
The formula for the volume of a cone is, V = 1/3 πr2 h
Substitute 8 for r and 18 for h.
V = 1/3 (3.1416) (8)2 (18)
≈ 1206.4
Therefore, the volume of the cone is about 1206.4 cubic centimeters.
Information Source: Varsity Tutors